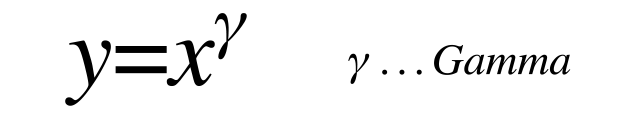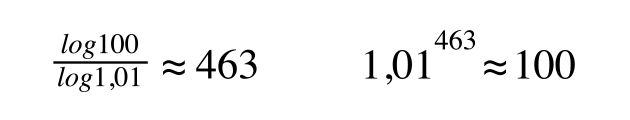Der Begriff »Gamma« ist sehr vielschichtig und lässt sich kaum eindeutig definieren, da er in diversen Disziplinen unterschiedlich benutzt wird. Dieser Artikel handelt ausschließlich von Gamma als Korrekturfunktion in der digitalen Bildbearbeitung und dessen historischen Hintergrund.

In der Bildbearbeitung definiert das Gamma das Verhältnis zwischen dem numerischen Wert eines Pixels und dessen tatsächlicher Leuchtdichte. Mathematisch gesehen sprechen wir beim Gamma von einer Potenzfunktion, deren Exponent eben Gamma genannt wird.



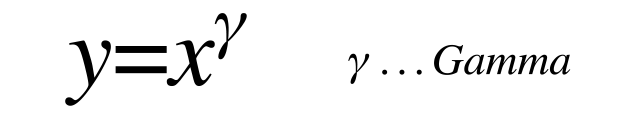
Wieso brauchen wir das Gamma?

Dafür gibt es einen historischen Grund, und dieser kommt aus der Fernsehtechnik. Bereits in den 40er-Jahren wurden zum Fernsehen Röhrenmonitore benutzt. Bei diesen »Cathode Ray Tube«- oder kurz CRT-Monitoren ist das Verhältnis zwischen der Eingangsspannung und der tatsächlich am Monitor resultierenden Leuchtdichte nicht linear. So erzeugt die Hälfte der maximalen Eingangsspannung am Monitor nicht 50%, sondern nur etwa 18% der maximal möglichen Leuchtdichte. Schuld daran ist die Arbeitsweise der Elektronenkanonen, die in den Röhrenmonitoren verbaut wurden.

Dieses nicht-lineare Verhalten lässt sich als Kurve (Potenzfunktion) darstellen. Die allermeisten CRT-Monitore weisen ein Verhalten auf, dass einem Exponenten, also Gammawert von ziemlich genau 2,5 entspricht. Wie hier an dem Graphen zu sehen, resultiert somit der Eingangswert 0,5 x in einer Leuchtdichte von nur 0,177 y.



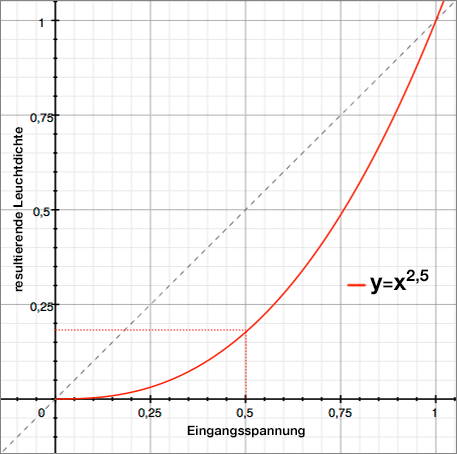
Das Bild wäre bei der Wiedergabe viel zu dunkel, daher wird es vorher künstlich aufgehellt, sodass sich die Korrektur und das Verhalten der Röhrenmonitore aufheben und letztlich ein (annähernd) lineares Verhalten erzeugen.
Bei dieser Korrektur spricht man von einer Gammakorrektur. Dazu wurde schon in den aus dem Jahr 1953 stammenden NTSC-Spezifikationen der Exponent für die Gammakorrektur mit 2,2 festgelegt.



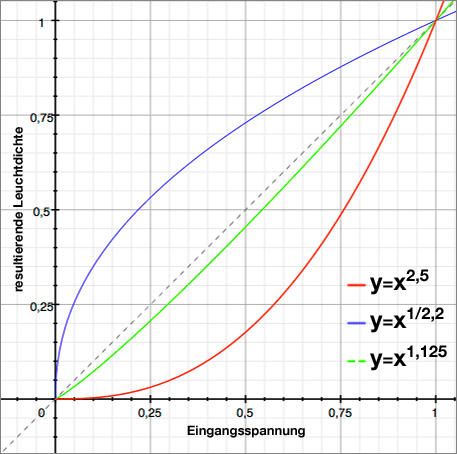
Wie man hier am Graphen erkennen kann, ist die aus der CRT-Kurve und Korrekturkurve resultierende Wiedergabekurve (grün) fast linear. Genau genommen weist sie noch ein effektives Gamma, auch Systemgamma genannt, von 1,13 auf – und das aus gutem Grund: Ferngesehen wird meist in einer halbdunklen Umgebung. Man stellte aber fest, dass ein komplett korrigiertes Bild in dieser Umgebung kontrastlos wirkt und entschied daher, dass das effektive Gamma zwischen 1,1 und 1,2 liegen sollte.

Ist die Gammakorrektur heute noch notwendig?

Das System »Gammakorrektur« stammt zwar aus Zeiten des analogen Fernsehens, hat aber in der digitalen Bildbearbeitung ebenso Gültigkeit. Immerhin wurden noch Anfang dieses Jahrhunderts CRT-Monitore als Computerbildschirme eingesetzt.

So weit, so gut. Doch heute benutzt niemand mehr Röhrenmonitore. Es stellt sich also die Frage, wie es mit LCD-Monitoren aussieht?
Moderne LCD-Monitore verhalten sich fast linear. Eine Gammakorrektur wäre daher eigentlich nicht mehr nötig. Man hat sich aber dazu entschlossen, Chips in den Monitoren einzubauen, die das Verhalten der CRT-Monitore quasi simulieren. Die Überlegung dahinter war, dass somit das komplette bestehende Bild- und Videomaterial aus CRT-Zeiten nicht unbrauchbar wird. Man hat sich also aus Kompatibilitätsgründen zu diesem Schritt entschlossen.

Jedes Bild, welches wir heute am Computer betrachten oder bearbeiten ist also aufgrund der alten CRT-Monitore gammacodiert. Die einzige Ausnahme sind 1-Bit-Bilder und unentwickelte Raw-Bilder. Allerdings werden letztere beim Entwickeln in Lightroom oder Camera Raw zwangsweise gammacodiert. Und das ist auch gut so, anderenfalls würde das Bild am Monitor nicht dem entsprechen, was wir ursprünglich beim Fotografieren wahrgenommen haben.

Mit welchem Gammawert ein Bild schließlich codiert ist, wird durch das eingebettete ICC-Profil festgelegt. AdobeRGB weist beispielsweise ein Gamma von 2,2 auf. An dieser Stelle möchte ich noch darauf hinweisen, dass wenn wir über das Gamma von Bildern sprechen, den Wert eigentlich verkehrt benutzen. Wenn wir von einem Bild mit einem Gamma von 2,2 sprechen, meint man damit eigentlich, dass das Bild so korrigiert wurde, dass es auf einem Monitor mit einem Gamma von 2,2 korrekt aussieht. Genau genommen lautet der Gammawert des Bildes somit 1 dividiert durch 2,2 – also etwa 0,45.

Technische Anmerkung: Bevor die Gammakorrektur angewandt wird, werden die Daten zuerst auf einen Wertebereich von 0 bis 1 skaliert. Das tolle daran ist, dass so die Endpunkte fix bleiben, da 0 und 1 hoch Gamma immer 0 und 1 bleiben. Der Kontrastumfang ändert sich also bei Gammakorrekturen nicht.
Hätten die ersten Röhrenmonitore ein lineares Verhalten aufgewiesen, wäre also nie die Notwendigkeit einer Gammakorrektur entstanden. Die Geschichte hat aber noch einen zweiten Teil:

Gamma und die Wahrnehmung des Menschen

Oft wird behauptet, dass die Gammakorrektur dafür benötigt wird, die nicht-lineare Wahrnehmung des Menschen zu kompensieren. Das ist falsch. Das Auge braucht keine Gammakorrektur. Auch wenn wir ein Bild malen, gibt es keine Gammakorrektur. Unser Auge sieht und soll auch immer die lineare Variante sehen. Die Gammakorrektur gleicht nur das nicht-lineare Verhalten der Monitore aus.

Es stimmt aber dennoch, dass unser Sehvermögen nicht linear arbeitet. Das heißt, das Licht von zwei Glühbirnen wird nicht als doppelt so hell empfunden wie das Licht von nur einer Glühbirne. Und das obwohl unsere Augen aus physikalischer Sicht natürlich doppelt so viele Photonen erreichen. Daraus folgt auch, dass das menschliche Sehvermögen viel sensibler gegenüber Änderungen in den dunklen als in den hellen Tönen ist. Anders ausgedrückt: Wir erkennen kleine Unterschiede zwischen dunklen Tönen besser als kleine Unterschiede zwischen hellen Tönen.



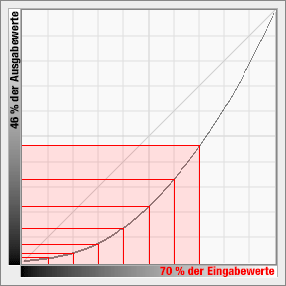
Diesen Umstand kann man sich zu nutze machen und schließlich durch die Gammacodierung Tonwerte effizienter speichern. Denn mithilfe der Gammafunktion werden die Tonwerte so verteilt, dass nicht zu viele Bits für die hellen Tonwertstufen verschwendet werden und noch genügend Bits für die dunklen Tonwertstufen übrig bleiben. Wie am Bild oben zu sehen, werden so beispielsweise für die dunkle Hälfte der Töne etwa 70% aller verfügbaren Tonwerte benutzt. Denn wie eben erwähnt, können wir Unterschiede in diesem Bereich besser unterscheiden. Doch was steckt hinter dieser Effizienzsteigerung?

Speichereffizienz durch Gammacodierung erhöhen (Gamma vs. Linear)

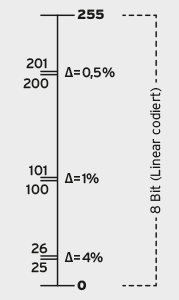
Das menschliche Sehvermögen reagiert bei einem gewissen Grad der Adaption auf ein Kontrastverhältnis von etwa 100:1. Innerhalb dieses Bereichs können wir einen Unterschied zwischen zwei Helligkeitsstufen wahrnehmen, wenn sich die Helligkeit um 1% vom Referenzwert unterscheidet. D.h. bei linearen 8-Bit-Daten (mit einem Wertebereich von 0 bis 255) können wir den Tonwert 100 von 101 unterscheiden, da dies einer Differenz von genau einem Prozent entspricht. Zwischen 200 und 201 sehen wir jedoch keinen Unterschied, da sich die beiden Tonwerte um nur 0,5% unterscheiden. Der Tonwert 201 hat also für unsere Wahrnehmung keinen Nutzen. Bei niedrigen Werten ist es aber genau umgekehrt: Der Unterschied zwischen 25 und 26 beträgt ganze 4%. Ein Verlauf würde in diesem Tonwertbereich deutliches Banding aufweisen, weil hier zu wenig Daten vorhanden sind. Man bräuchte die Zwischenwerte 25,25, 25,5 und 25,75, um einen stufenlosen Verlauf zu erzeugen. Diese sind aber in 8-Bit-Daten nicht vorhanden. Und genau hier liegt das Problem von linear-codierten Daten: Die Tonwerte sind in Bezug auf unsere Wahrnehmung ineffizient verteilt.

Eine Lösung wäre nun das Verwenden von 16-Bit-Daten, welche genug Abstufungen bereitstellen, sodass dieses Problem für unsere Wahrnehmung keine Rolle mehr spielt. Doch bevor wir nun die lineare Codierung mit größerer Bittiefe verwenden (und somit mehr Speicherplatz benötigen), können wir auch weniger Tonwertstufen mit nicht-linearer Codierung benutzen:

Die Kontrastensibilität des Auges beträgt, wie bereits erwähnt, etwa 1%. Für eine lineare Codierung benötigt man daher etwa 9900 Tonwerte, um ein Kontrastverhältnis von 100:1 abzubilden. Der Grund: 1% vom niedrigsten Wert 1 beträgt 0,01. Mit dieser Schrittweite geht es bis zum höchsten Wert 100. Für die 9900 erforderlichen Tonwerte benötigt man somit mindestens 14 Bit. Allerdings ist das verschwenderisch, denn wir erkennen den Unterschied ja nur in den dunkelsten Bereichen, also sehr niedrigen Tonwerten. Beispielsweise beträgt die Differenz vom Wert 10 auf den nächsten Wert, also 10,01, nur noch 0,1%. Dieser Unterschied ist für unser Auge nicht mehr wahrnehmbar. Wenn man nun davon ausgeht, dass die Kontrastsensibilität über den gesamten Kontrastumfang immer 1% beträgt, könnte man die Luminanz auch logarithmisch codieren. Für ein Kontrastverhältnis von 100:1 braucht man so nur noch 463 Tonwerte. (Im Download-Bereich befindet sich zur einfachen Darstellung dieses Unterschiedes ein Excel-Dokument.)

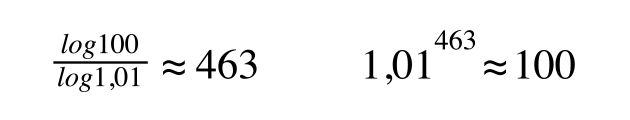
Für 463 Tonwerte benötigt man aber immer noch mindestens 9 Bit. Nach dem »Rec. 709 Standard« ist aber auch ein Kontrastverhältnis von 50:1 für das Fernsehen ausreichend, sodass wir bei den heute üblichen 8 Bit angelangt sind.

Die logarithmische Codierung basiert auf der Annahme, dass die Kontrastsensibilität über einen großen Kontrastumfang gleich bleibt. Diese Annahme ist aber nicht ganz richtig. Eine Potenzfunktion stellt eine deutlich bessere Annäherung an die Kontrastsensibiliät unserer Wahrnehmung dar. Und somit sind wir wieder beim Gamma angelangt.

All das hat zwar natürlich mit der Wahrnehmung des Menschen zu tun, war aber nicht der ursprüngliche Grund für die Gammakorrektur, denn Röhrenmonitore gab es schon lange bevor wir Bilder und Videos digital speicherten. Es handelt sich hier also bloß um einen erwünschten Nebeneffekt, der dafür sorgt, dass 8-Bit-Bilder für die allermeisten Zwecke ausreichen und Banding somit weitgehend verhindert wird.

Gamma in der Praxis

Bis jetzt haben wir ausschließlich die Theorie betrachtet. In der Praxis hat das Gamma aber heutzutage einen eher untergeordneten Wert. Denn das Colormanagement kümmert sich automatisch um die Umwandlung zwischen den verschiedenen Gamma-Werten von Bildern oder Monitoren, sodass wir immer eine korrekte und konstante Helligkeitsverteilung sehen. Das Gamma ist also ein weitgehend »unsichtbarer« Prozess.

Auch bei der Monitorkalibration ist der Gammawert nicht von allergrößter Bedeutung, da wie gesagt das Colormanagement-System ohnehin jegliche Differenzen ausgleicht. Natürlich macht es aber Sinn, für die Kalibrierung ein Gamma zu wählen, welches dem am häufigsten benutzten RGB-Farbraum entspricht. Arbeitet man beispielsweise fast ausschließlich mit ProPhoto RGB macht es Sinn, auf ein Gamma von 1,8 hin zu kalibrieren. Arbeitet man eher mit AdobeRGB, ist es besser ein Gamma 2,2 zu benutzen. So werden Rundungsfehler klein gehalten oder im besten Fall komplett vermieden.

Die Gammawerte der verschiedenen RGB-Profile können unter anderem auf der Webseite von Bruce Lindbloom nachgeschlagen werden.

Quellen:
Poynton, Charles: Digital Video and HDTV Algorithms and Interfaces. San Francisco, Morgan Kaufmann Publishers, 2003.

Tweet

Tags: ICC-Farbprofil, Bittiefe, Gamma