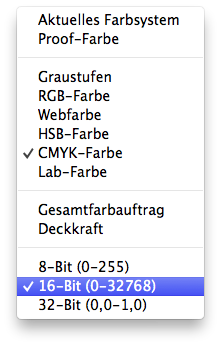
Photoshop bietet die Möglichkeit, 16-Bit-Daten zu verarbeiten. Allerdings nur nominell, denn intern handelt es sich dabei um sogenannte 15+1 Bit »unsigned« (vorzeichenlos). Die Werte reichen daher nicht von 0 bis 65535, wie es bei echten 16 Bit theoretisch möglich wäre, sondern von 0 bis 32768 (32769 Werte). Auch das ist aber eine Besonderheit, da mit »normalen« 15 Bit nur ein numerischer Wert zwischen 0 und 32767 darstellbar ist. Das 16. Bit wird also nur für den letzten Wert (32768) benötigt. 16 Bit heißt also nicht, dass der maximale Wert 65536 ist, sondern nur, dass die Werte 16 Bit benötigen, um repräsentiert zu werden.
Der Grund für diese Arbeitsweise ist, dass es dadurch eine definierte Mitte gibt. 50 % fällt somit auf einen definierten Wert und nicht, wie in 8 Bit, zwischen zwei Werte. Das ist beispielsweise für die Berechnung der Füllmethoden wichtig.
8 Bit: 255 / 2 = 127,5
16 Bit : 65535 / 2 = 32767,5
15+1 Bit: 32768 / 2 = 16384
Diese Arbeitsweise erlaubt aber auch schnellere Berechnungen, da hiermit sogenannte bitweise Verschiebungen – Bitshifts – möglich sind (anstatt von echten Divisionen).
Ein Bitshift ist ein Befehl, der eine bestimmte Anzahl von Bits um eine gewisse Stellenanzahl nach links oder rechts verschiebt (shiftet).
Beispiel:
1000000000000000 = 32768
0100000000000000 = 16384
Die Zahl wurde durch das Verschieben der Bits durch 2 dividiert. Werden die Bits nach rechts verschoben, wird vorne einfach mit Nullen aufgefüllt. Der Performancegewinn gegenüber einer echten Division ist
ca. 30:1.
Warum aber sind diese Divisionen so wichtig? Das liegt an der Mathematik hinter all diesen Operationen. Denn oft müssen die Werte normalisiert werden und dazu muss eben mit dem Maximalwert (255 oder 32768) dividiert werden. Chris Cox hat das so formuliert:
In integer (or fixed point) math, many operations have to normalize the range. So you frequently have to divide by the maximum value (255, 32768, or 65535). Dividing by 255 can be done with a few shifts and adds instead of a very slow divide instruction. Dividing by 32768 can be done with a single shift. Dividing by 65535 requires quite a few more shifts and adds, or multiplication (by an inverse), shifts, and adds, or a very slow divide instruction — but no matter how you tackle it, it’s going to be a lot slower than a single shift.
[Korrektur 1. Juni 2015: Kleine Fehler ausgebessert; Zitat eingefügt]
Tags: Bittiefe, Bits und Bytes